解答
100円玉n枚と500円玉n枚を投げた時
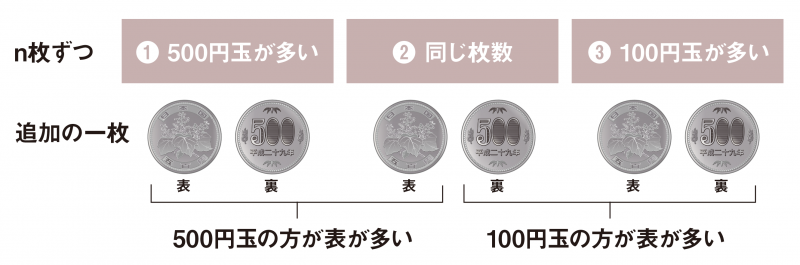
①500円玉の方が表が多い
②表の枚数が同じ
③100円玉の方が表が多い
の3つのケースがあり得ます。
この時、対称性から①と③の確率は同じです。
その後もう一枚500円玉を投げ、これを加えた時、500円玉の方が表が多くなるのは
「①の時または②で追加の一枚が表だった時」
逆に、500円玉の方が表が多くならないのは、
「③の時または②で追加の一枚が裏だった時」
①、③の確率は同じで、②の時も追加の一枚で表が出るか裏が出るかも半々です。
つまりどちらも確率は同じなので、500円玉の方が表が多い確率は1/2です。
どうやったら思いつけるようになるのか?~踏み込んだ解説~
確率を考えるうえでは大別して以下の二つの考え方があります。
①組合的確率(今求めたい事象のパターン数と、パターンの総数を数え上げ、比をとる)
②測度的確率(事象ごとの確率を定め、その関係から目的とする事象の確率を求める)
この問題はパターン数が数えられますから、まず①を考えてみましょう。
①のアプローチで求めたいパターンを地道に計算するなら、
・100円玉がk枚表、500円玉がk+1枚以上表になる確率を求め、和をとる。
・100円玉がk枚以下表、500円玉がk+1枚表になる確率を求め、和をとる。
等が考えられます。これでもちゃんと解けますが、どちらも繁雑です。
では②はどうでしょうか?ここで重要なのは、「何と何が同じ確率で起きるのか?」に注目することです。これを「同様に確からしい」と言います。今回はn枚とn+1枚で条件が対称でないですから、100円玉と500円玉で表が多くなる確率は異なります。そこで、まずn枚ずつだったらどうか、と考えることになるわけです。n枚ずつなら勝つ確率と負ける確率は同じになる。ではこれにあと一枚加えるとどうなるか…。
ここまでくれば、独立・排反・条件付確率の概念がしっかり整理されていれば、比較的容易に上記の答案に達することができるはずです。これら3つの概念については、場合の数・確率講義の4日目に詳しく扱います。